Jasmine Hollis

Jasmine Hollis

Biography

Jas Hollis (he/they) is a rising junior at Yale University studying atmosphere, ocean, and climate dynamics. He has worked on projects involving Arctic Ocean properties and cloud physics. Post-college, Jas plans to pursue a PhD in atmospheric science, with goals of researching convective storm dynamics and engaging in climate policy work. They have experience in database management with SQL, machine learning with Python, working as a writing consultant for college applicants, and tutoring students in C, C++, and MATLAB. He is also conversational in French and Mandarin Chinese. Beyond academics, they sing for a collegiate a cappella group, serving separate terms as the group’s business and album manager. Finally, Jas is passionate about community betterment, which led them to spend a few summers serving their community through a feed-and-read program in San Antonio, TX, and to study queer history and social justice. Jas hopes to center societal impact in his future pursuits, using his research and leadership skills to advance outreach in atmospheric science and inform tangible climate change solutions

Abstract

A Simple Analytic Approximation for Single-Raindrop Precipitation Efficiency

Precipitation efficiency (η) describes the fraction of raindrop water molecules that reach the Earth’s surface. Though critical to understanding the water cycle, precipitation efficiency remains poorly represented within current weather and climate models. In this project, we derive a simple, analytic approximation of precipitation efficiency as a function of surface relative humidity, surface air temperature, and initial radius of the raindrop. Through our process, we assume a dry-adiabat in the subcloud layer and a monodisperse population of raindrops. Here is our resulting approximation:

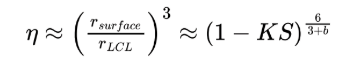
In this approximation, precipitation efficiency scales with the cubed ratio of initial raindrop
radius remaining at the surface to initial radius at the cloud base. K is the effective evaporative
cross-section of the raindrop, meaning the area undergoing evaporation, adjusted to account for
ventilation. S is the effective saturation deficit, which captures the thermodynamic potential for
evaporation, based on relative humidity and temperature. Finally, we assess the approximation
using numerical simulations of the exact equations. In future work, we will extend the
approximation to account for a range of initial raindrop sizes. Overall, our approximation of
precipitation efficiency will improve our understanding of the water cycle.